Project Home

H1 Prototype

Mechanicals

Electronics

Software

Heliostat Mechanicals - Geometry

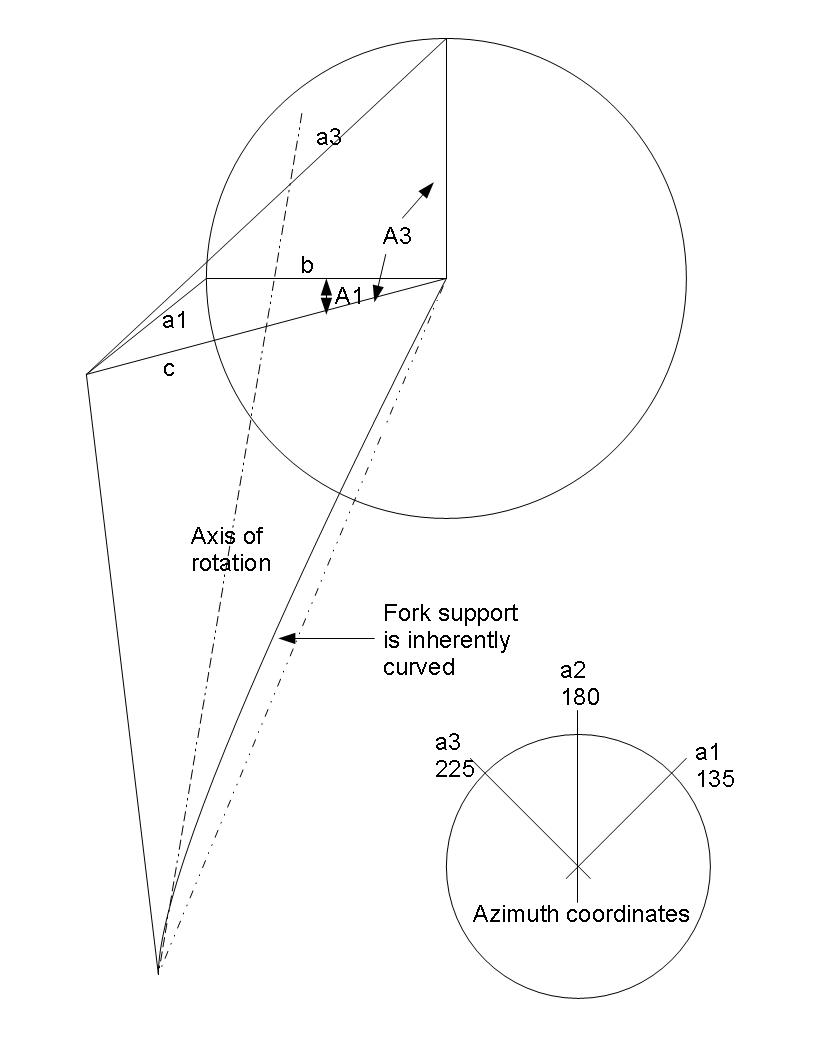
The first issue to be considered is the ideal location of the linear actuator for the desired range of motion. Secondly, but most importantly: the resultant equation of motion so that the miror angle may be calculated based on the actuator position.
Some be inclined to point out that a linear actuator can be used to obtain even more than 360 degrees of linear rotation if desired as well as a linear rate of rotation, through the use of a pully and belt. This may well have its own advantages, however accuracy, as we will see, will be fine even with non-linear rotation from using a traditional pushrod style solution.

Lets define the range of motion:
Azimuth Axis - depending on latitude and season, the azimuth angle of the sun may actually change more than 180 degrees in the course of a day, and a linear actuator pushrod is incapable of achieving 180 degrees in practice; however, we must keep in mind that the heliostat angle always bisects the solar and target angles, thus we only need half the solar azimuth range. Thus if the target were always directly ahead, 90 degrees of motion would be adequate; however, to design a heliostat which is capable of multiple targets, we need a bit more.
Allowing for targets to be +/- 30 degrees from the north-south axis only requires 120 degrees of motion. A geometrical treatment of the situation will reveal that the ideal location of the actuator base falls on a line connect the end points of two tangential radii, and that 120 degrees is an ideal range of motion to minimize the decrease in resolution at the extremes of motion.

Altitude Axis - the altitude axis only goes from 0 to 90, and the bisecting angle would only need a range of 45; however a couple of special positions need to be kept in mind: park, and clean. A park position pointed straight up should generally avoid having the reflection go in an unwanted direction (at least for typical residential applications). The resulting horizontally level position makes an easy way of calibrating the position. Likewise, having a cleaning position which puts the mirrors in a vertical orientation not only facilitates maintenance, but also provides another crucial calibration point.
Allowing for targets to be +/- 15 degrees requires only slight motion past vertical. This also provides for the ability to compensate for any inherent pitch angle due to the frame mounting.

Knowing the desired range of rotation, and the range of motion the linear actuator is capable of, we can calculate the ideal radius (b) of the actuator fulcrum (C), as well as the position of the actuator base(B). This defines two sides of a triangle. Side c remains completely fixed, while side (b) remains fixed in length, but pivots about point (A), as required by changes in the value of side (a). The law of cosines, which states that the ratios of the sides and the cosine of their respective angles are equal, lets us solve the angle (A) based on the known sides.